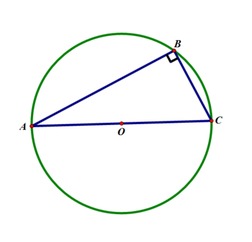
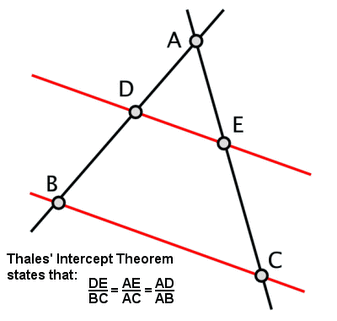
The majority of the work the Greek did with mathematics was geometry based. One of the big names in Greek geometry (and Greek's first great mathematician) was Thales. Thales was one of the first people to define guidelines for the development of geometry and worked with some ideas we commonly see today (like similar triangles and right triangles). Thales also developed and proved a theorem named after himself. Thales Theorem states:
Another well known Greek Mathematician was Euclid. Euclid did a lot of work in the realm of mathematical proofs.
While I am on the topic of mathematical proofs, that is another concept we can attribute to the great Greek mathematicians. The Greek were some of the first people to look for ways to definitively prove or disprove mathematical theorems. Civilizations prior to Greece tended to use inductive reasoning by finding several examples that worked and using that as a general rule to follow while performing mathematical calculations. However, the Greek used deductive reasoning by use of logical mathematical steps that followed directly from a set of given axioms to determine the truth of a statement. I would argue that this is the greatest accomplishment in the world of mathematics the Greeks (or anyone else) has given modern mathematics. Undeniable proof is what gives math is power. Mathematical proof shows that given the right circumstances a theorem is true always, and there is so much power to that. It allows us to know, without a doubt, that it "works." Not only does a proof allow us to know that a particular theorem is always true, but it also paves the way to use that proof as step in another proof to prove another theorem. Writing proofs is one of my favorite aspects of mathematics because of the power they hold. And a proof allows us to understand the math at a new level. At this level of math, it isn't about the numbers, it's about the patterns which is incredible considering that so many non-math majors just think math is just numbers - in reality math goes so much deeper than "just numbers."
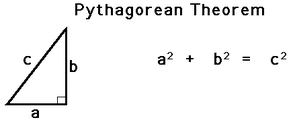
 RSS Feed
RSS Feed
