Roman numerals - we have all seen them. You know, the numbers made up of l's, V's, and X's (as well as some others). But how much do we all really know about these numbers? We're they efficient for arithmetic? How easy are they to read and understand? Let's first establish what exactly this number system is. The Roman numerals consist of seven basic symbols that each represent a value.
Subtraction feels like "cancelling" to me in this system. If you stack the two values with the larger value on top you can "cancel" numerals that are the same. Again, you might have to decompose some to be able to cancel. Let's try XVl-V. Here, the V's cancel leaving us Xl. Not to bad, but what about LXXXl-Lll? Here we can cancel the L's, but we need to take away two l's from the first value but we only have one.
LXXXl - Lll
LXXVllllll - Lll
(cancel L's and two l's)
XXVllll
XXlX
It's pretty clear that this arithmetic can get rather long and hard to follow -and I'm not even going to try to get into multiplication and division. Not to mention Roman numerals had no concept for zero, and could not be used to calculate fractions.
In 1202, Leonardo of Pisa, A.K.A. Fibonacci, brought the Hindu Arabic number system to Europe (which was then using the Roman numeral system). This new system contained the figures 1, 2, 3, 4, 5, 6, 7, 8, 9, and the use of 0. Using these 10 figures any number could be written. He wrote the "Book of Calculation" to promote the use of this new system in Europe. In this book he explained the Hindu Arabic system and essentially taught readers how much easier and compact arithmetic could be, as well as how to use this new system using detailed examples.
This new system was base ten. As in ten 1's were replaced by one 10, ten 10's were replaced by one 100, ten 100's were replaced by one 1,000 and so on. Also, this new system introduced the idea of place value where the first digit represented how many 1's were in the number, the second digit represented how many 10's, the third digit represented how many 100's. For example, 1427 has one 1,000, four 100's, two 10's, and seven 1's. But what do we do it we don't have any of a particular value? We use the new symbol zero. So, the number 703 means there are zero 10's.
We all know how addition and subtraction work in this system. For addition, just add the two numbers and regroup up to the next place value when you reach ten in one place value. In subtraction, just subtract the number of 1's in one number from the other, then the number of 10's, and so on, regrouping to get 10 of a smaller place value from a larger place value when necessary.
So, which would you rather write,
CCXClV or 294?
DCCCXVlll or 817?
MMCMXCVlll or 2998?
It's pretty clear that the Hindu Arabic system is more efficient and easier to use. Despite this, it took quite a while to catch on in 13th century Europe. However, it is now the most common symbolic representation of numbers in the world. Can you imagine a modern world where we are still using the old Roman numeral system? Think of how different our processes of math would be. What about advanced math topics like calculus, would they even be possible with such a clunky system? We often associate Fibonacci with the famous Fibonacci sequence, yet very rarely hear his name associated with the number system we use today.
So, the next time you do some basic arithmetic or work with large numbers, stop and be thankful for the number system we have today. If it wasn't for Fibonacci we might still be writing with X's, V's, and l's - and I know that I am glad that is not the case!

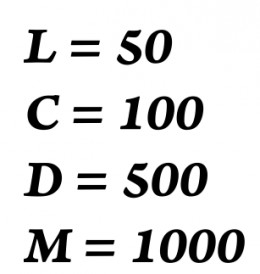

 RSS Feed
RSS Feed
